
يعرَّف المقياس من خلال الغرض منه، ويتلخَّص في تحديد مواقع الأفراد حسب نوع السمة أو درجة امتلاكهم لها.
1 – المقياس الاسمي: Nominal Scale (يصنَّف ولا يرتَّب):
هو أبسط أنواع المقاييس، يدلُّ على النوع ولا يدلُّ على الكم البعض لا يعتبره من المقاييس، وظيفة هذا النوع هو المساعدة في عمليَّة التصنيف والترتيب والتنظيم، حيث إنَّ الأعداد تعطى عشوائياً للمتغيرات وليس لها دلالة كميَّة، وإنما تقوم مقام الأسماء، كما يعتمد على تصنيف موضوع القياسات إلى فئات تبعاً لاشتراكها في سمة واحدة مثلاً (1= رجال، 2= نساء، رقم طالب 1352]، التخصص الجامعي( رياضيات ، فيزياء ، …) مثال آخر: الأرقام الموجودة على قمصان فريق كرة القدم فقط هي لتصنيف اللاعبين ولا يمكن أن نقول بأن اللاعب رقم (10) أو أقوى مرتين من اللاعب رقم (5)، وهذا المقياس يعطي معلومات محدودة جداً عن الظاهرة المقاسة، بحيث يبيَّن مدى توفُّر خاصيَّة معينة في المتغيّر. ومن الأمثلة على ذلك أيضاً: الجنس- الجنسيَّة- الحالة الاجتماعيَّة- فصيلة الدم (A، B، AB، O) – نوع الوقود المستخدم في السيارة- شركة الطيران التي يفضَّل التعامل معها-مكان الإقامة- نوع المدرسة.
فمثلا عند ترميز البيان الخاص بالجنس في بحث معيَّن يعطي الذكور عادة رقم 1 والإناث رقم 2، الأرقام هنا تفيد التمييز بين الذكور والإناث فقط، ولا تدل على تفوّق أو تفضيل الذكور على الإناث أو العكس. مثال آخر على البيانات الاسميَّة، الأسئلة التي تظهر في كثير من الاستبيانات وتأخذ إجابة نعم أو لا، مثلا عندما يسأل عن موافقة المواطنين على إعطاء المرأة حقوقها السياسيَّة يعطى عادة عند تبويب أو ترميز هذا السؤال بالحاسب الآلي رقم 1 للإجابة بنعم ورقم 2 للإجابة بلا.
إنَّ العمليَّة الحسابيَّة الوحيدة التي يمكن تطبيقها على المقاييس الاسميَّة (التصنيفيَّة) هي عمليَّة العد، ولا يمكن استخدام أيَّة عمليَّة أخرى كالجمع أو الطرح أو الضرب أو القسمة.
2 – المقياس الرتبي: Rank scale (يصنف ويرتب لكن لا يبين الفرق):
هو المقياس الذي يمكننا من ترتيب أفراد المجموعة تصاعدياً أو تنازلياً حسب امتلاكهم لسمة معيَّنة فهو يمتلك خاصيَّة التصنيف والترتيب، لكن هذا المقياس لا يبيِّن الفرق في العلامة الخام بين طالب وآخر.
مثال (ممتاز ـ جيد جداً..ِ… إلخ) (الأول ـ الثاني ـ الثالث) فقد يكون بين الأول والثاني درجة وبين الثاني والثالث عشرة. هذا المقياس يستخدم بكثرة في الميول والاتجاهات (الموسيقى، الخط، الرسم).
وهذا المقياس يعطي معلومات عن التفاوت بين الأشياء من حيث الوصف فقط، وليس الحجم مثلاً يمكن ترتيب البيان الخاص بتقديرات طلبة الجامعة إلى: F- 1,D- 2, C- 3, B- 4, 5- A وهذا الترتيب يفيد الوصف بمعنى أن تقدير F أعلى من التقدير D ولكن لا يعني ذلك أن تقدير F يعادل ضعف التقدير Dمن أمثلة البيانات الرتبيَّة:
-المستوى التعليمي لمجموعة من الأفراد (1. ثانويَّة عامَّة 2. مؤهَّل دبلوم 3. شهادة جامعيَّة 4. دراسات عليا).
– الدرجات الوظيفيَّة لمجموعة من الموظفين في سلم الوظائف العامَّة (1. الدرجة الأولى 2. الدرجة الثانية. 3. الدرجة الثالثة. 4. الدرجة الرابعة……).
– الترتيب العام لفرق الدوري الانجليزي (1. مانشستر يونايتد 2. ارسنال 3. ليذر يونايتد 4. سندرلاند 5. ليفربول……).
– رضاء عملاء البنك الوطني عن الخدمات المقدمة إليهم (1. راضي تماما 2. راضي 3. غير متأكد 4. غير راضي 5. غير راضي تماما).
وهو المقياس الذي يمكننا من ترتيب أفراد المجموعة تنازلياً او تصاعدياً حسب درجة امتلاكهم لسمة معيَّنة كمقياس ليكرت أيضاً (أوافق بشدة- أوافق- محايد-معارض-معارض بشدة).
الأعداد في هذا المقياس تشير إلى الترتيب وليس إلى الكم الذي تحويه. والمسافات في هذا المقياس لا تكون متساوية. أي مقياس الرتب يشتمل على فئات تحمل معنى الترتيب ولا تحمل معنى التساوي.
وفي هذا المقياس يرتب الأفراد حسب امتلاكهم للسمة او الخاصيَّة المقيسة. أي يدل هذا المقياس على أن الفرد أو المجموعة يمتلكون من السمة أو الخاصيَّة المطلوب قياسها دونما العلم بالفرق بين أي اثنين من هؤلاء الأفراد.
كما يمتلك هذا المقياس خاصيَّة الترتيب بالإضافة إلى خاصيَّة التصنيف التي يمتلكها المقياس الاسمي لأنه لا يكتفي بأن يبين اختلاف الأفراد بالنسبة لسمة معينة(الاسمي) بل ويرتبهم أيضاً حسب درجة امتلاكهم لهذه السمة.
3 – مقياس المسافة Distance scale (الفترة): (يصنف ويرتب ويبين الفرق):
أدق من المقياسين السابقين، فالأرقام هنا تحمل معنىً كمياً نستطيع معرفة كميَّة الصفة والفرق في كميتها بين شيء وآخر فهو يستخدم للبيانات الكميَّة. مثلاً: المسافة بين 3 و4 درجات مئويَّة هو نفسه الفرق بين المسافة بين 98و99 درجات مئويَّة. وهو يقيس الصفات بطريقة غير مباشرة لذا فهو مناسب للأمور التربويَّة والنفسيَّة، ويمكننا من معرفة الفرق بين درجة (أ وب).
لكن الوحدات في هذا المقياس متساوية لأن الدرجة 89-90 قاست مستوى عقلياً مرتفعاً بينما الدرجة 29-30 قاست مستوى عقلياً متدنياً.
كما أن الصفر هنا افتراضي أي أنه لا يعني انعدام السمة. مثلاً في حال قلنا درجة الحرارة هي صفر درجة مئويَّة فإن هذا لا يعني انعدام الحرارة من الوجود إنما نقصد أن الجو بارد جداً.
ملاحظة: (هناك مقدار معين تضعه المؤسَّسة للتعبير عن الصفر الافتراضي 25 % أو 30 % من الدرجة الكليَّة، عندنا في الجامعة 40%).
على سبيل المثال: إذا أخذنا مقياس الفهرنهايت نجد أنَّ درجة تجمُّد الماء هي 32 درجة وليس الصفر، وبالتالي لا يمكننا القول بأن 100 درجة فهرنهايت تساوي 50 درجة فهرنهايت مرتين لأنَّ المقياس نفسه لا يبدأ من الصفر. الصفر في المقياس الفتري ليس صفراً حقيقياً وإنما صفر منسوب أو افتراضي، فمثلاً يوجد لدينا مقياسين لدرجة الحرارة المقياس المئوي والمقياس الفهرنهايتي. لا يمكننا الاعتماد على النسب في المقياس الفتري فعندما تكون درجة الحرارة 40 فهرنهايت لا يعني أنَّها تساوي ضعف الحرارة عند درجة 20 مئوي.
مثال:
إذا كانت درجة حرارة الجو في واشنطن 80.6 فهرنهايت فما هي درجة الحرارة بالمئويَّة.
الحل:
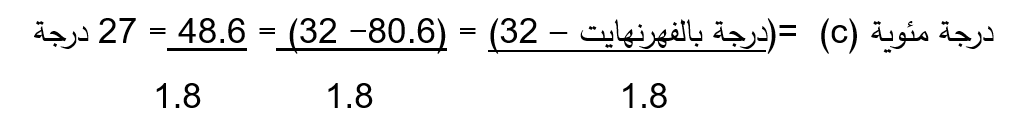
يعطي هذا المقياس معلومات عن التفاوت بين الأشياء من حيث الوصف والحجم. هذا المقياس يملك خاصيَّة الفواصل أو المسافات المتساوية التي تفصل بين درجة وأخرى مجاورة لها، بحيث أن وجود خاصيَّة المسافات المتساوية بين كل درجتين متجاورتين يعني إمكانيَّة إجراء بعض العمليات الحسابيَّة كالجمع والطرح.
وبالنهاية يمكن أن نلخَّص هذا المقياس كالآتي:
- القياس بهذا المستوى أرقى من القياس بمستوى الرتبة.
- تحتمل الأرقام في هذا المقياس معنىً كمياً.
- يتمتَّع هذا المقياس بوحدات متساوية.
- إنَّ القياسات التي تؤخذ على مقياس المسافات تزودنا بمعلومات حول كل من الترتيب والكميَّة النسبيَّة للسمة المقيسة.
- الأعداد لها معنىً وترتيب.
- المسافات بين الأعداد متساوية.
- لا يوجد صفر حقيقي في هذا المقياس وإنَّما يتضمَّن صفراً اعتباطياً(عرفياً) لا يمثِّل غياب السمة المقيسة. من أمثلة هذا المقياس: درجة الحرارة.
4 ـ مقياس النسبة: Ratio_ Scale
هذا المقياس يقيس بطريقة مباشرة، وله صفر حقيقي (مطلق) يمثِّل غياب السمة المقاسة، بشكل يمكن الباحث من معرفة النسب واختلافها بين مختلف العناصر بسهولة، فالباحث يمكنه الإشارة إلى عنصر بأنَّه أقوى مرتين من العنصر الآخر مثلاً: شخص ما لديه حساب في بنك وحسابه صفر فالمقصود هنا هو انعدام أي شيء من حسابه، كما أنَّ وحدات هذا المقياس متساوية، ويقيس النواحي الفيزيائيَّة، ونستطيع هنا إجراء جميع العمليات الحسابيَّة، وسميت نسبة أي (نسبة إلى الوحدة 1). وهو أدق المقاييس، لأنَّه يمكن استخدام ومعرفة ومقارنة النسب من خلاله.
في هذه الحالة يبيِّن المقياس القيمة الحقيقيَّة للظاهرة المدروسة، فمثلا يمكن رصد البيان الخاص بأوزان خمسة أفراد كما يلي: – 76.5 كجم – 70 كجم – 85 كجم.
يزودنا هذا المقياس بمعلومات حول الترتيب ويتميَّز هذا المقياس بأنَّ له وحدات متساوية وصفراً مطلقاً (حقيقياً) يمثِّل غياب السمة المقاسة فالصفر في المقاييس النسبيَّة حقيقي ،وبالتالي يتمّ أخذ النسب، فالطول 180 هو ضعفي الطول 90، أما الوزن صفر فيعني انعدام الوزن أي غياب السمة. من أمثلة هذا المقياس الطول، الوزن، العمر، مقدار الأموال في البنك، عدد أفراد المجتمع أو مجموعة ما، الوقت الذي تم استخدامه لإنهاء مهمة ما، الدخل، سنوات التدريس، الدرجات في الاختبار.
نجد أن كل مقياس يمتلك خصائص المقياس الذي قبله ويزيد عليه خاصيَّة تميِّزه. ومن هنا جاءت فكرة هرميَّة المقاييس بالاعتبار.
__________
*الدكتورة ميادة القاسم- الأستاذ المساعد في مناهج وطرائق البحث الاجتماعي قسم علم الاجتماع – جامعة ماردين – حلب سابقاً.
اكتشاف المزيد من التنويري
اشترك للحصول على أحدث التدوينات المرسلة إلى بريدك الإلكتروني.






